Home | Raytracing Reference | Help
A scaling transformation changes the size of an object. An object may be scaled by different factors in the different coordinate directions. The set of scaling factors is called a "scale vector". For example, the scale vector (2, 1, 1) doubles the length of the object in the x-direction but leaves the other two dimensions unchanged. A scaling transformation can be represented in matrix form. If the object is to be scaled by the factors sx, sy and sz in the 3 coordinate directions with respect to the reference point P(x0, y0, z0), then the required matrix is
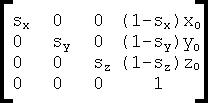
A scene consists of all the elements of a 3-D environment, including objects, light sources, bounding volumes and animation paths.
A shader is a function that describes the appearance of an object. Nearly all rendering programs implement the basic ambient-diffuse-Phong shader. Shaders can be used to generate innumerable effects, from photorealistic renderings to engineering drawings to cartoon-style images. Pixar Animation Studios, the creators of the the Renderman Interface Specification, were instrumental in the development of the technique of allowing users to specify their own shaders for describing surfaces, lights, volumes etc. This method has the advantage of freeing the creator of the main rendering program from having to write code for every special effect the program may have to support. Instead, the user creates his/her own shader modules tuned to his/her own requirements.
A shadow is a region which does not receive light. Usually, the term is used in the more general sense of a region which receives less light than its surrounding areas. Raytracers calculate shadows by sending out shadow rays towards light sources and testing if any object blocks this ray. Other algorithms use "shadow maps". This technique renders views of a scene as seen from the light source positions. All the points visible from these positions receive light, the rest are in shadow. Indexed images of these renderings are called "shadow maps" and are used to identify shadow area in the actual rendering process.
A shadow ray is a ray that has its origin at a surface point and travels towards a light source. It is used by rendering programs (especially raytracers) to determine whether the surface point is in shadow or not. If the shadow ray intersects any objects lying between the point and the light source, then the path of light is blocked and the point is in shadow. If the blocking object is translucent, then the light intensity is attenuated by the transmittivity of the object and the point is partially shadowed.
A soft shadow is a shadow produced when an object blocks a light source having non-zero dimensions. Such a shadow has a soft, fuzzy border that fades from dark to light instead of a sharp edge.
See also: area light
Space subdivision is an efficiency scheme that reduces object-intersection calculations in a raytracer by dividing the scene into a number of distinct regions. The usual division methods include grid and octree subdivision. Grid subdivision divides the scene into an array of boxes, each containing a subset of all the objects in the scene. Octrees follow the same principle by dividing the scene into eight octants (formed by slicing a cuboid along three planes parallel to the three coordinate planes), and recursively subdividing any octants which have too many objects. Once the space subdivision has been carried out, the raytracer treats each sub-region as a bounding volume. In a grid, we test to see if the ray intersects a grid cell. If it does, then we perform intersection calculations with the objects inside the cell, otherwise we ignore these objects altogether. In an octree, we find the intersected octants, then the intersected sub-octants in each, and so on until we reach the terminal nodes. This gives us a pruned list of objects that are likely candidates for intersection.
See also: Bounding Volume Hierarchy (BVH)
Specular surfaces are perfect reflectors of light. Mirrors show specular reflection. "Specular highlights" (a bit of a misnomer) are bright spots produced on shiny surfaces that are approximately specular. Phong highlights model this effect. In fact, the terms "specular" and "Phong" are often used interchangeably to describe the parameters used (as in specular/Phong coefficient or specular/Phong exponent).
A sphere is a perfectly round 3-dimensional object that is defined as the locus of a point that remains at a constant distance, known as the "radius", from a fixed point, known as the "centre". A sphere is a quadric: in 3-D Cartesian coordinates, it has the equation
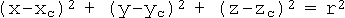
where (xc, yc, zc) are the coordinates of the centre and r is the radius.
A spline is, simply, a curve. Before the advent of CAD programs and the like, engineers and draftsmen used to model curves by hanging adjustable weights from different points on a flexible strip. This curved strip was called a spline. Nowadays, splines are defined mathematically and are described with control points and boundary conditions. The control points are the analogue of the weights, they may be thought of as gravitational attractors, pulling a section of the curve in a particular direction. There are many mathematical models of splines, including basic cubic splines, cardinal splines, Hermite splines, bezier curves, B-splines, beta splines and NURBS. Usually, splines are divided into two broad groups: interpolation and approximation splines. Interpolation splines (e.g. cardinal splines) actually pass through the control point positions. Approximation splines (such as Bezier curves) bend towards control points, but do not necessarily pass through them. Given n + 1 control points, most spline curve equations have the parametric form
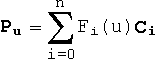
where Pu is the position vector of the point on the curve with parameter u, Fi(u) is the ith function in a set of n + 1 functions of u known as "basis functions", and Ci is the position vector of the ith control point.
A spline patch is a curved surface, defined by two independent spline functions. It may be thought of a set of splines whose control points are generated by another spline function. It is usually designed using a (m + 1) x (n + 1) grid of control points. Given two sets of basis functions fi(u) and gj(v), where i varies from 0 to m and j varies from 0 to n, the spline patch may be described in parametric form as
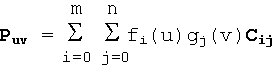
where Puv is the point on the surface with parameters u, v and Cij is the position vector of the control point at position (i, j) in the grid.
See also: bicubic patch
A subdivision surface is a curved surface formed by recursively subdividing a grid of control polygons until it approximates a smooth surface. The subdivision process usually generates points on the basis of some spline function. A subdivision surface is thus like a spline patch, but has more flexibility due to the fact that the original grid need not be rectangular. An example of a subdivision scheme is the Catmull-Clark method.
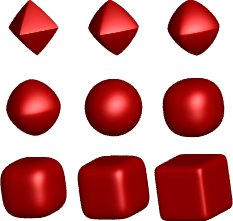
A superquadric is a shape created by introducing one (if 2-D) or two (if 3-D) extra parameters in the standard quadric equation. As an illustration, let's consider the superellipsoids, closed surfaces generated by modifying the ellipsoid equation
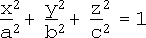
The introduction of two parameters e1 and e2 yields the superellipsoid equation
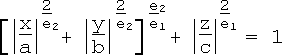
For e1 = e2 = 1, we have the ordinary ellipsoid. Superellipsoids may also be described with the parametric equations