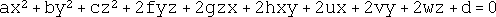Home
| Raytracing Reference
| Help
FuzzyPhoton
Q - Raytracing Reference
A
| B
| C
| D
| E
| F
| G
| H
| I
| J
| K
| L
| M
| N
| O
| P
| Q
| R
| S
| T
| U
| V
| W
| X
| Y
| Z
Quadratic
Quadric
Quartic
Quadratic
A quadratic is a second-degree polynomial. One may encounter quadratic expressions or quadratic equations. A quadratic expression f(x) is usually written as
f(x) = ax^2 + bx + c
where a, b, c are real constants and a is not 0. The graph of y = f(x) in 2-D Cartesian coordinates is a parabola. A quadratic equation is written as
f(x) = 0, i.e
ax^2 + bx + c = 0
The roots p and q of this equation are given by
p = (-b - sqrt(b^2 - 4ac)) / 2a
q = (-b + sqrt(b^2 - 4ac)) / 2a
The roots are real only when b^2 - 4ac is positive (or zero, in which case there is only one root). In terms of the graph of y = f(x), the roots are the values of x at which the parabolic graph intersects the x-axis. Quadric shapes such as circles, ellipses, parabolas, spheres, cylinders, hyperboloids etc all give quadratic equations when their intersections with a ray are considered. Therefore solving quadratic equations is a common function in a raytracer.
Quadric
A quadric is a locus in 3-dimensional space that can be represented in Cartesian coordinates as a polynomial equation in x, y and z of the second degree. It is the 3-D analog of a conic (circle, ellipse, parabola, hyperbola, pair of straight lines). The general quadric equation may be written as
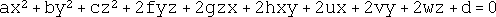
When this equation represents a non-empty locus, it can be reduced by translation and rotation to one of the following "canonical forms":
i. Ellipsoid (including sphere): 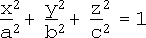
ii. Hyperboloid of 1 sheet: 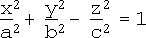
iii. Hyperboloid of 2 sheets: 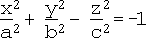
iv. Elliptic paraboloid: 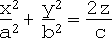
v. Hyperbolic paraboloid: 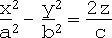
vi. Quadric cone: 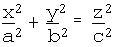
vii. Elliptic cylinder: 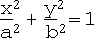
viii. Hyperbolic cylinder: 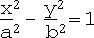
ix. Parabolic cylinder: 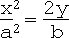
x. Pair of non-parallel planes: 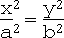
xi. Pair of parallel planes: 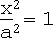
xii. Plane: 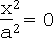 , i.e. x = 0
, i.e. x = 0
xiii. Line: 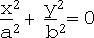 , i.e. x = y = 0
, i.e. x = y = 0
xiv. Point: 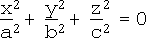 , i.e. x = y = z = 0
, i.e. x = y = z = 0
Forms i, ii, iii, iv and v are the "non-degenerate quadrics".
Quartic
A quartic is a polynomial of degree 4. Often, quartic refers to a shape described as a polynomial function of the coordinates (say x, y, z), such that the highest degree of any term is 4. An example of such a shape is a torus. A quartic equation is an equation of the form f(x) = 0, where f(x) is a quartic polynomial. The method of solving this equation is due to the Italian mathematician Ludovici Ferrari. It consists of adding the term (mx + b)^2 to both sides of the equation so as to convert them into perfect squares (m and b are calculated with some algebraic acrobatics followed by the solution of a cubic equation). We now equate the square roots of these quantities with the two possible combinations of positive/negative signs (same sign or different signs). This gives us two quadratic equations. Solving these equations gives us the 4 roots (real or complex, distinct or repeated) of the quartic equation.
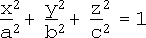
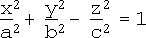
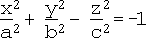
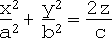
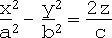
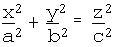
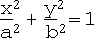
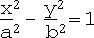
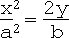
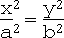
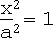
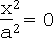 , i.e. x = 0
, i.e. x = 0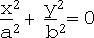 , i.e. x = y = 0
, i.e. x = y = 0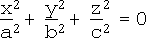 , i.e. x = y = z = 0
, i.e. x = y = z = 0