
Home | Raytracing Reference | Help
A matrix is a rectangular array of numbers. An m x n matrix has m rows and n columns (note that some people think of it as m columns and n rows). For example, a 3x4 matrix might be
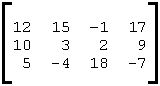
Matrices may be added to, subtracted from or multiplied by other matrices. The matrix product A * B exists when the number of columns of A and the number of rows of B are equal. It is calculated on a row * column basis. For example,

Matrices may also be multiplied by scalars. More information on matrix operations is easily available in a high school mathematics textbook or on the Net.
The immense usefulness of matrices in graphics software is due to the fact that a matrix can represent a simple transformation such as rotation, translation or scaling. For example, the matrix representing a translation by tx, ty and tz units in the x, y and z directions respectively in 3-D space looks like

A composite transformation may be formed by multiplying matrices. For example, the matrix product A * B * C corresponds to the sequence (note the order): perform transformation C, then B, then A. If A was a translation matrix, B was a scaling matrix and C was a rotation matrix, then the sequence would be "rotate-scale-translate". This gives a compact and convenient way of specifying complex transformations: a sequence of 1000 transformations takes up exactly the same space a a single one.
A 4x4 matrix may be used to transform a position vector (x, y, z) to a new position (x', y', z') by matrix multiplication as follows:
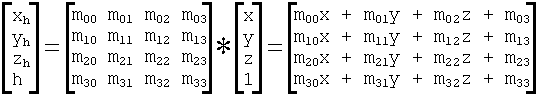
This gives the transformed vector in "homogenous coordinates" as (xh, yh, zh, h). This is converted to standard vector form by dividing by h. Therefore we have
(x', y', z') = (xh / h, yh / h, zh / h).
The "inverse" of a square matrix A is another square matrix inv(A) such that A * inv(A) = inv(A) * A = I, where I is the identity matrix (main diagonal elements are 1, rest are 0) of the same size as A. The inverse of a transformation matrix represents the inverse transformation. For example, if A is a matrix to rotate a point around the x-axis by 90 degrees, then inv(A) is a matrix to rotate a point around the x-axis by 90 degrees in the opposite direction.
A mesh is a collection of polygons (usually triangles or quadrilaterals). Meshes are most useful when these polygons share edges, forming a continuous sheet. Meshes can approximate just about any surface. This makes them very convenient for rendering difficult shapes like spline patches. At low enough resolutions and with fake curve smoothing techniques like Phong shading, a mesh representation can be indistinguishable from the real curved surface (see picture). Most 3-D programs store a mesh of many polygons in such a way that it takes up less memory than an equal number of independent polygons.

A model is a way of representing an object using methods other than the original. Models need not be scale replicas of material objects. Physicists use mathematical models of real-world phenomena. Computers use models of data structures and relationships, learning systems may be modelled with neural nets. Models may be static or procedural. In most cases, they are simple, manageable and analysable versions of the originals. Geometrical models, used in graphics, are often modelled with equations. When simple equations are not available, mesh or volumetric models may be used.
See also: lighting model
Monte Carlo is a town on the Riviera hosting a famous casino, where your bank balance, unless you are specially gifted, depends entirely on the laws of chance. This inspired the use of the name to imply any form of random sampling used in computers. For example, the use of jitter in antialiasing is a Monte Carlo method, since it introduces random variations within the grid restriction. A method of global illumination, because of its implicit dependence on random sampling, has almost monopolized the use of the word "Monte Carlo" to describe itself. This method is an alternative to radiosity, and models multiple interdiffuse reflections by sending out rays in random scattering directions from a surface point and averaging the intensities obtained.
A rendered frame is usually like a still photograph taken with infinitely fast film -- all the objects appear to be motionless. Such frames give no indication of the speed and direction of moving objects, and result in jerky animation. Actually, a frame represents a definite time-interval -- just as a real photograph captures everything in the scene within the exposure time. Look at a photo of, say, a racing car taken sideways on. The image of the car will be blurred because its position changes rapidly all the while that the shutter is open. This feature is known as "motion blur". The blurred image may be thought of as the superimposition of the images of all the intermediate positions of the car. Ideally, we'd want an infinite number of intermediates to accurately model motion blur, but computers have to make do with less. The exact number depends on the velocities of the objects, the exposure time and the precision required. Frames of the scene at intermediate times are rendered and merged into a single motion-blurred frame.